Journal of Statistics: Advances in Theory and Applications[1] R. Balka, Z. Buczolich and M. Elekes, Topological Hausdorff
dimension and level sets of generic continuous functions on fractals,
Chaos Solitons Fractals 45(12) (2012), 1579-1589; MR3000710.
[2] J. R. Christensen, Measure theoretic zero sets in infinite
dimensional spaces and applications to differentiability of Lipschitz
mappings, Publ. Dep. Math. 10(2) (1973), 29-39; MR0361770.
[3] J. R. Christensen, Topology and Borel Structure, North-Holland
Publishing Company, Amsterdam, 1974; MR0348724.
[4] J. Cohen, The earth is round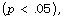 
American Psychologist 49(12) (1994),
997-1003.
[5] R. Dougherty, Examples of non-shy sets, Fund. Math. 144 (1994),
73-88; MR1271479.
[6] H. L. Lavoie, S. A. Mulaik and J. H. Steiger, What if there were
no Significance Tests?, Lawrence Erlbaum Associates, 1997.
[7] B. R. Hunt, T. Sauer and J. A. Yorke, Prevalence: A
translation-invariant “almost every†on
infinite-dimensional spaces, Bulletin (New Series) of the American
Mathematical Society 27(2) (1992), 217-238; MR1161274.
[8] Kaisan High Accuracy Calculation, Cauchy distribution
(percentile)
http://keisan.casio.com/has10/SpecExec.cgi
[9] A. B. Kharazishvili, Topologicheskie aspekty teorii mery,
(Russian), [Topological Aspects of Measure Theory] Naukova Dumka,
Kiev, 1984; MR0784614.
[10] L. Kuipers and H. Niederreiter, Uniform Distribution of
Sequences, Wiley-Interscience [John Wiley & Sons], New
York-London-Sydney, 1974; MR0419394.
[11] J. Mycielski and S. Swierczkowski, On the Lebesgue measurability
and the axiom of determinateness, Fund. 54 (1964), 67-71;
MR0161788.
[12] J. Mycielski, Some unsolved problems on the prevalence of
ergodicity, instability, and algebraic independence, Ulam Quart. 1(3)
(1992), 30 ff., approx. 8 pp. (Electronic only); MR1208681.
[13] E. Nadaraya, On non-parametric estimates of density functions and
regression curves, Theor. Prob. Appl. 10 (1965), 186-190.
[14] J. Nunnally, The place of statistics in psychology, Educational
and Psychological Measurement 20(4) (1960), 641-650.
[15] G. R. Pantsulaia, On separation properties for families of
probability measures, Georgian Math. J. 10(2) (2003), 335-342;
MR2009981.
[16] G. R. Pantsulaia, Invariant and quasiinvariant measures in
infinite-dimensional topological vector spaces, Nova Science
Publishers Inc., New York, 2007; MR2527890.
[17] G. Pantsulaia, On a certain partition of the non-locally compact
abelian Polish group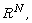 
Proc. A. Razmadze Math. Inst. 149 (2009),
75-86; MR2597356.
[18] G. Pantsulaia and M. Kintsurashvili, Why is null hypothesis
rejected for “almost every†infinite sample by some
hypothesis testing of maximal reliability?, Journal of Statistics:
Advances in Theory and Applications 11(1) (2014), 45-70.
http://www.scientificadvances.co.in
[19] G. Pantsulaia and M. Kintsurashvili, An effective construction of
the strong objective infinite sample well-founded estimate, Proc. A.
Razmadze Math. Ins. 166 (2014), 113-119.
[20] G. Pantsulaia and M. Kintsurashvili, An objective infinite sample
well-founded estimates of a useful signal in the linear
one-dimensional stochastic model, Rep. Enlarged Sess. Semin, I. Vekua
Appl. Math. 28 (2014), (Accepted).
[21] M. Rosenblatt, Remarks on some nonparametric estimates of a
density function, Textit. Ann. Math. Statist. 27 (1956), 832-837;
MR0079873.
[22] E. F. Schuster, Estimation of a probability density function and
its derivatives, Ann. Math. Statist. 40 (1969), 1187-1195;
MR0247723.
[23] Albert N. Shiryaev, Problems in Probability, Translated by Andrew
Lyasoff, Problem Books in Mathematics, Springer, New York, 2012;
MR2961901.
[24] S. Solecki, On Haar null sets, Fund. Math. 149(3) (1996),
205-210; MR1383206.
[25] R. M. Solovay, A model of set theory in which every set of reals
is Lebesgue measurable, Ann. Math. 92 (1970), 1-56; MR0265151.
[26] I. Sh. Ibramkhallilov and A. V. Skorokhod, On Well-off Estimates
of Parameters of Stochastic Processes (in Russian), Naukova Dumka,
Kiev, 1980.
[27] Z. Zerakidze, G. Pantsulaia and G. Saatashvili, On the separation
problem for a family of Borel and Baire G-powers of
shift-measures on R, Ukrainian Math. J. 65(4) (2013), 470-485;
MR3125005.
