Journal of Statistics: Advances in Theory and Applications
FOR THE THREE PARAMETER DAGUM DISTRIBUTION[1] M. Ali and J. Woo, Inference on reliability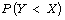 
in a p-dimensional Rayleigh
distribution, Mathematical and Computer Modeling 42 (2005a),
367-373.
[2] M. Ali and J. Woo, Inference on 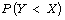in a Pareto distribution, Journal of
Modern Applied Statistical Methods 4 (2005b), 583-586.
[3] M. Ali, M. Pal and J. Woo, Inference on 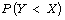in generalized uniform distributions,
Calcutta Statistical Association Bulletin 57 (2005), 35-48.
[4] M. Ali, M. Pal and J. Woo, Estimation of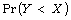 
when X and Y belong to
different distribution families, Journal of Probability and
Statistical Science 8 (2010), 35-48.
[5] M. Ali, J. Woo and M. Pal, Inference on reliability 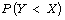in two-parameter exponential distributions,
International Journal of Statistical Sciences 3 (2004), 119-125.
[6] E. A. Amin, Bayesian and non-Bayesian estimation of 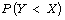from type I generalized logistic
distribution based on lower record values, Journal of Applied Sciences
Research 8(1) (2012), 118-125.
[7] A. P. Basu, Estimates of reliability for some distributions useful
in reliability, Technometrics 6 (1964), 215-219.
[8] M. A. Beg, On the estimation of 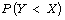for two-parameter exponential distribution,
Metrika 27 (1980), 29-34.
[9] C. Kleiber and S. Kotz, Statistical Size Distribution in Economics
and Actuarial Sciences, John Wiley & Sons, Inc., Hoboken, NJ, 2003.
[10] C. Kleiber, A guide to the Dagum distribution, modeling income
distributions and Lorenz curves economic studies in equality, Social
Exclusion and Well-Being 5 (2008), 97-117.
[11] C. Quintano and A. D’Agostino, Studying inequality in
income distribution of single-person households in four developed
countries, Rev. Income Wealth 52(4) (2006), 525-546.
[12] Dagum ditribution, Comm. Statist. Simulation Comput. 36(6)
(2007), 1187-1199.
[13] C. Dagum, A model of income distribution and the conditions of
existence of moments of finite order, Bulletin of the International
Statistical Institute, 46 (Proceedings of the 40th Session of the ISI,
Warsaw, Contributed Papers), (1975), 199-205.
[14] C. Dagum, A new model of personal income distribution:
Specification and estimation, Economie Appliqufiee 30 (1977),
413-437.
[15] C. Dagum, The generation and distribution of income, the Lorenz
curve and the Gini ratio, Economie Appliqufiee 33 (1980a), 327-367.
[16] C. Dagum, Generating systems and properties of income
distribution models, Metron. 38 (1980b), 3-26.
[17] F. Downtown, The estimation of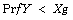 
in the normal case, Technometrics 15
(1973), 551-558.
[18] F. Domma, S. Giordano and M. Zenga, The Fisher information matrix
in doubly censored data from the Dagum distribution, Working Paper No.
8, Department of Economics and Statistics, University of Calabria,
Italy, 2009.
[19] F. Domma, G. Latorre and M. Zenga, Reliability studies of the
Dagum distribution, Working Paper No. 207, Department of Quantitative
Methods for Economics and Business, University of Milan - Bicocca,
Italy, 2011.
[20] Francisco J. Rubio and Mark F. J. Steel, Bayesian inference for
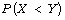using asymmetric dependent distributions,
Journal of Bayesian Analysis 7(3) (2012), 771-792.
[21] V. V. Ivshin, Unbiased estimators of 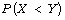and their variances in the case of uniform
and two-parameter exponential distributions, Journal of Mathematical
Sciences 81 (1996), 2790-2793.
[22] K. Iwase, On UMVU estimators of 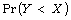in the 2-parameter exponential case,
Memoirs of the Faculty of Engineering, Hiroshima University, 9 (1987),
21-24.
[23] G. D. Kelley, J. A. Kelley and W. R. Suchany, Efficient
estimation of 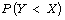in the exponential case, Technimetrics 18
(1976), 359-360.
[24] M. Masoom Ali, Manisha Pal and Jungsoo Woo, Estimation of
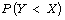in a four-parameter generalized gamma
distribution, Austrian Journal of Statistics 41(3) (2012), 197-210.
[25] J. I. McCool, Inference on 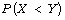in the Weibull case, Communications in
Statistics: Simulation and Computation 20 (1991), 129-148.
[26] M. Pal, M. Ali and J. Woo, Estimation and testing of 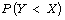in two parameter exponential
distributions, Statistics 39 (2005), 415-428.
[27] M. Z. Raqab and D. Kundu, Comparison of different estimators of
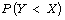for a scaled Burr Type X distribution,
Communications in Statistics: Simulation and Computation 34 (2005),
465-483.
[28] M. Z. Raqab, M. T. Madi and D. Kundu, Estimation of 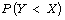for a 3-parameter generalized exponential
distribution, Communications in Statistics: Theory and Methods 37
(2008), 2854-2864.
[29] S. Rezaei, R. Tahmasbi and M. Mahmoodi, Estimation of 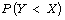for generalized Pareto distribution,
Journal of Statistical Planning and Inference 140 (2010), 480-494.
[30] Studies in Inequality, Social Exclusion and Well-Being, Vol. 5,
C. Duangkamon, Editor, Springer, New York, NY, 2008.
[31] H. Tong, A note on the estimation of 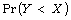in the exponential case, Technometrics 16
(1974), 625.
[32] H. Tong, On the estimation of 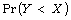for exponential families, IEEE
Transactions on Reliability R-26 (1977), 54-56.
[33] A. Wong, Interval estimation of 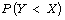for generalized Pareto distribution,
Journal of Statistical Planning and Inference 142 (2012), 601-607.
