Journal of Algebra, Number Theory: Advances and Applications
[1] B. Anglès, Units and norm residue symbol, Acta Arith. 98(1)
(2001), 33-51.
[2] C. Batut, K. Belabas, D. Bernardi, H. Cohen and M. Olivier, PARI
GP 2.0.12 Alpha Power PC Version, Université Bordeaux I,
1989-1998.
[3] H. Brückner, Explizites Reziprozitätsgesetz und Anwendungen,
Vorlesungen Fachberich Math. Univ. Essen, Heft 2 (1979), 83.
[4] A. Granville, The Kummer-Wieferich-Skula Approach to the First
Case of Fermat’s Last Theorem, Gouvêa, Fernando (ed.) et
al., Advances in Number Theory, The Proceedings of the Third
Conference of the Canadian Number Theory Association, Clarendon Press,
Oxford, (1993), 479-497.
[5] G. Gras, Class Field Theory: From Theory to Practice, SMM,
Springer-Verlag, 2003; Second corrected printing, 2005.
[6] G. Gras, Analysis of the classical cyclotomic approach to
Fermat’s last theorem, Publ. Math. de Besançon, Algèbre
et Théorie des Nombres, Actes de la Conférence Fonctions
L et arithmétique, Besançon 2009; Presses Universitaires
de Franche-Comté (2010), 85-119.
[7] G. Gras and R. Quême, Vandiver papers on cyclotomy revisited
and Fermat’s last theorem, Publ. Math. de Besançon,
Algèbre et Théorie des Nombres, Presses Universitaires de
Franche-Comté (2012), (to appear).
[8] K. Hatada, Chi-square tests for mod 1 distribution of Fermat and
Fibonacci quotients, Sci. Rep. Fac. Educ., Gifu Univ., Nat. Sci. 12
(1988), 1-2; Mod 1 distribution of Fermat and Fibonacci quotients and
values of zeta functions at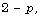 
Comment. Math. Univ. St. Pauli 36 (1987),
41-51.
[9] H. Koch (A. N. Parshin, I. R. Shafarevich and R. V. Gamkrelidze,
Eds.), Number Theory II, Algebraic Number Theory, Encycl. Math. Sci.,
Vol. 62, Springer-Verlag, 1992; Second printing: Algebraic Number
Theory, Springer-Verlag, 1997.
[10] M. Kurihara, Some remarks on conjectures about cyclotomic fields
and k-groups of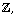 
Compositio Math. 81 (1992), 223-236.
[11] P. Mihăilescu, On Vandiver’s Best Result on FLT1,
Nonlinear Analysis: Stability, Approximation and Inequalities- A
Volume Dedicated to the 60th Anniversary of Themistocles M. Rassias,
G. Georgiev, P. Pardalos and H. M. Srivastava (Editors),
Springer-Verlag, New York, 2012.
[12] S. Sitaraman, Vandiver revisited, J. Number Theory 57(1) (1996),
122-129.
[13] S. Sitaraman, On a Fermat type Diophantine equation, J. Number
Theory 80(2) (2000), 174-186.
[14] S. Sitaraman, Note on a Fermat type Diophantine equation, J.
Number Theory 99(1) (2003), 29-35.
[15] H. S. Vandiver, A property of cyclotomic integers and its
relation to Fermat’s last theorem, Ann. Math. 21 (1919/1920),
73-80.
[16] H. S. Vandiver, Application of the Theory of Relative Cyclic
Fields to both Cases of Fermat’s Last Theorem, Transaction of
the AMS 28 (1926), 554-560; Application of the Theory of Relative
Cyclic Fields to both Cases of Fermat’s Last Theorem (second
paper), Transactions of the AMS 29 (1927), 154-162.
[17] L. C. Washington, Introduction to Cyclotomic Fields, Second
Edition, Springer-Verlag, 1997.
