Journal of Algebra, Number Theory: Advances and Applications[1] M. A. Bennett, Powers in recurrence sequences: Pell equations,
Transactions of the American Mathematical Society 357 (2004),
1675-1691.
[2] A. Bremner and N. Tzanakis, Lucas sequences whose 12th or 9th term
is a square, J. Number Theory 107 (2004), 215-227.
[3] Y. Bugeaud, M. Mignotte and S. Siksek, Classical and modular
approaches to exponential Diophantine equations, I, Fibonacci and
Lucas perfect powers, Annals of Math. 163 (2006), 969-1018.
[4] J. H. E. Cohn, Perfect Pell powers, Glasgow Mathematical Journal
38(1) (1996), 19-20.
[5] H. Darmon and L. Merel, Winding quotients and some variants of
Fermat’s last theorem, J. Reine Angew. Math. 490 (1997), 81-100.
[6] T. Kagawa and N. Terai, Squares in Lucas sequences and some
Diophantine equations, Manuscripta Math. 96 (1998), 195-202.
[7] M. Le, On the Diophantine equation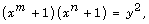 
Acta Arithmetica 82(1) (1997), 17-26.
[8] P. Mihailescu, Primary ciclotomic units and a proof of Catalan’s
conjecture, J. Reine Angew. Math. 572 (2004), 167-195.
[9] P. Ribenboim and W. L. McDaniel, The square terms in Lucas
sequences, J. Number Theory 58 (1996), 104-122.
