Journal of Algebra, Number Theory: Advances and Applications[1] E. A. Bender, O. Patashnik and H. Rumsey Jr., Pizza slicing,
Phi’s, and the Riemann hypothesis, Amer. Math. Monthly 101
(1994), 307-317.
[2] P. Bundschuh, Einführung in die Zahlentheorie, Springer Verlag,
1988.
[3] Encyclopedic Dictionary of Mathematics, Nihon Sugakkai, English
Translation of the Third Edition, M.I.T. Press, 1987.
[4] Encyclopedia of Mathematics, Vol. 9 ed.-in-Chief I. M. Vinogradov,
Updated and Annotated English Translation, Kluwer Acad. Publ.,
Dordrecht, 1993.
[5] Loo-Keng Hua, Introduction to Number Theory, Springer Verlag,
1982.
[6] A. E. Ingham, Review 3954, A. M. S. Reviews 28 (1964).
[7] A. Ivić, The Riemann Zeta-Function, John Wiley and Sons,
1985.
[8] N. M. Korobov, Estimates of trigonometrical sums and their
applications (in Russian), Uspekhi Mat. Nauk. 13(4) (1958),
185-192.
[9] N. M. Korobov, Exponential Sums and their Applications, Kluwer
Acad. Press, Dordrecht, 1992.
[10] Y.-F. S. Pétermann, On an estimate of Walfisz and Saltykov for
an error term related to the Euler function, J. Theorie des Nombres de
Bordeaux 10 (1998), 203-236.
[11] S. S. Pillai and S. D. Chowla, On the error terms in some
asymptotic formulae in the theory of numbers I, J. London Math. Soc.
5 (1930), 95-101.
[12] H.-E. Richert, Zur Abschätzung der Riemannschen Zetafunktion
in der Nähe der Vertikalen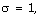 
Math. Ann. 169 (1967), 97-101.
[13] A. I. Saltykov, On Euler’s function (in Russian), Vestnik
Moskov. Univ., Ser. I Mat. Meh. (1960), 34-50.
[14] E. C. Titchmarsh and (Revised by) D. R. Heath-Brown, The Theory
of the Riemann Zeta-Function, Second Edition, Clarendon Press, Oxford,
1986.
[15] I. M. Vinogradov, A new estimate of the function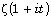 
(in Russian), Izv. Acad. Nauk. SSSR Ser.
Mat. 22 (1958), 161-164.
[16] I. M. Vinogradov, Trigonometrical Sums in Number Theory, Stat.
Publ. Soc. Calcutta, 1975.
[17] I. M. Vinogradov, The Method of Trigonometric Sums in Number
Theory, Second Edition, Moscow 1980 in: Selected Works, Springer
Verlag, 1985.
[18] A. Walfisz, Über die Wirksamkeit einiger Abschätzungen
trigonometrischer summen, Acta Arith. 4 (1958), 108-180.
[19] A. Walfisz, Weylsche Exponentialsummen in der Neueren
Zahlentheorie, VEB Deutscher Verlag der Wissenschaften, Berlin, 1963.
