Journal of Algebra, Number Theory: Advances and Applications
ARE UNIQUELY DETERMINED BY THEIR ELEMENT
ORDERS AND THEIR ORDER[1] O. A. Alekseeva and A. S. Kondratiev, Recognizing groups
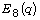by the element orders, Ukr. Math. Zh. 54(7)
(2002), 1003-1008.
[2] O. A. Alekseeva and A. S. Kondratiev, Quasirecognizability of a
class of finite simple groups by the set of element orders, Sib. Math.
Zh. 44(2) (2003), 241-255.
[3] R. Brandl and W. J. Shi, The characterization of PSL (2,
q) by their element orders, Journal of Algebra l63 (1994),
109-114.
[4] J. H. Conway et al., An Atlas of Finite Groups, Clarendon Press,
Oxford, 1985.
[5] M. A. Grechkoseeva, W. J. Shi and A. V. Vasil’ev, Recognition by
spectrum of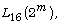 
Algebra Colloq. 14(4) (2007), 585-591.
[6] G. Higman, Finite groups in which every element has prime power
order, J. London Math. Soc. 32 (1957), 335-342.
[7] V. D. Mazurov, Characterization of finite groups by the sets of
orders of their elements, Algebra and Logic 36(1) (1997), 23-32.
[8] Wujie Shi, A new characterization of some simple groups of Lie
type, Contemporary Math. 82 (1989), 171-180.
[9] Wujie Shi, On an E. Artin’s problem, Acta Math. Sinica 35(2)
(1992), 262-265, (in Chinese).
[10] A. V. Vasil\\\'ev and M. A. Grechkoseeva, On recognition of the
finite simple orthogonal groups of dimension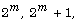 
and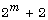 
over a field of characteristic 2, Siberian
Mathematical Journal 45(3) (2004), 420-432.
[11] A. V. Vasil’ev and E. P. Vdovin, An adjacency criterion for the
prime graph of finite simple groups, Algebra and Logic 44(6) (2005),
381-406.
[12] A. V. Vasil’ev, On connection between the structure of a finite
group and the properties of its prime graph, Siberian Mathematical
Journal 46(3) (2005), 396-404.
[13] A. V. Vasil’ev and M. A. Grechkoseeva, On recognition by
spectrum of finite simple linear groups over fields of characteristic
2, Siberian Mathematical Journal 46(3) (2005), 593-600.
[14] J. S. Williams, Prime graph components of finite groups, Journal
of Algebra 69 (1981), 489-513.
[15] Mingchun Xu and Wujie Shi, Pure quantitative characterization of
finite simple groups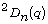 
and 
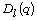(l odd), Algebra Colloq. 3 (2003),
427-443.
[16] K. Zsigmondy, Zur Theorie der Potenzreste, Monatsh. Math. Phys. 3
(1892), 265-284.
