Journal of Algebra, Number Theory: Advances and Applications[1] T. Becker and V. Weispfenning, Gröbner Bases, Springer-Verlag,
1993.
[2] B. Buchberger, Gröbner bases: An algorithmic method in
polynomial ideal theory, Multidimensional Systems Theory (N. K. Bose,
ed.), Reidel Dordrecht, (1985), 184-232.
[3] E. L. Green, Non-commutative Gröbner bases and projective
resolutions, Proceedings of the Euroconference Computational Methods
for Representations of Groups and Algebras, Essen, 1997, (Michler,
Schneider, eds), Progress in Mathematics, Vol. 173, Basel, Birkhauser,
Verlag, (1999), 29-60.
[4] D. Hartley and P. Tuckey, Gröbner bases in Clifford and
Grassmann algebras, J. Symb. Comput. 20 (1995), 197-205.
[5] A. Kandri-Rody and V. Weispfenning, Non-commutative Gröbner
bases in algebras of solvable type, J. Symb. Comput. 9 (1990),
1-26.
[6] H. Li and F. Van Oystaeyen, Zariskian Filtrations, K-Monographs in
Mathematics, Vol. 2, Kluwer Academic Publishers, 1996.
[7] H. Li, Y. Wu and J. Zhang, Two applications of non-commutative
Gröbner bases, Ann. Univ. Ferrara - Sez. VII - Sc. Mat. 45 (1999),
1-24.
[8] H. Li and F. Van Oystaeyen, A Primer of Algebraic Geometry, Marcel
Dekker, Inc., New York, Basel, 2000.
[9] H. Li, Non-commutative Gröbner Bases and Filtered-Graded
Transfer, LNM, 1795, Springer-Verlag, 2002.
[10] H. Li,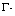 
leading homogeneous algebras and Gröbner
bases, Advanced Lectures in Mathematics, International Press and
Higher Education Press, Boston-Beijing, 8 (2009), 155-200.
[11] H. Li, On the calculation of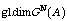 
and 
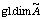by using Gröbner bases, Algebra Colloquium
16(2) (2009), 181-194.
[12] T. Mora, An introduction to commutative and non-commutative
Gröbner bases, Theoretic Computer Science 134 (1994), 131-173.
[13] P. Nordbeck, On some basic applications of Gröbner bases in
non-commutative polynomial rings, Gröbner Bases and Applications,
Vol. 251 of LMS Lecture Note Series, Cambridge Univ. Press, Cambridge,
(1998), 463-472.
