Journal of Algebra, Number Theory: Advances and Applications[1] J. Ax, Zeroes of polynomials over finite fields, American Journal
of Mathematics 86(2) (1964), 255-261.
DOI: https://doi.org/10.2307/2373163
[2] M. Artin and B. Mazur, Formal groups arising from algebraic
varieties, Annales Scientifiques de l’École Normale
Supérieure, 4e Série 10(1) (1977), 87-131.
DOI: https://doi.org/10.24033/asens.1322
[3] T-H. Bülles, Fulton’s trace formula for coherent
cohomology, Preprint, Available from.
http://www.math.uni-bonn.de/people/huybrech/Buelles.pdf
[4] P. Berthelot, S. Bloch and H. Esnault, On Witt vector cohomology
for singular varieties, Compositio Mathematica 143(2) (2007),
363-392.
DOI: https://doi.org/10.1112/S0010437X06002533
[5] P. Berthelot, H. Esnault and K. Rülling, Rational points over
finite fields for regular models of algebraic varieties of Hodge type
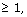Annals of Mathematics 176(1) (2012),
413-508.
DOI: https://doi.org/10.4007/annals.2012.176.1.8
[6] M. Brion and S. Kumar, Frobenius Splitting Methods in Geometry and
Representation Theory, Progress in Mathematics, Birkhäuser,
2005.
[7] A. Chatzistamatiou, On the Frobenius stable part of Witt vector
cohomology, Mathematische Annalen 354(3) (2012), 1177-1200.
DOI: https://doi.org/10.1007/s00208-011-0769-6
[8] B. Chiarellotto, Rigid cohomology and invariant cycles for a
semistable log scheme, Duke Mathematical Journal 97(1) (1999),
155-169.
DOI: https://doi.org/10.1215/S0012-7094-99-09707-7
[9] B. Chiarellotto and C. Lazda, Combinatorial degenerations of
surfaces and Calabi-Yau threefolds, Algebra and Number Theory 10(10)
(2016), 2235-2266.
DOI: https://doi.org/10.2140/ant.2016.10.2235
[10] B. Chiarellotto and B. Le Stum, Pentes en cohomologie rigide et
F-isocristaux unipotents, Manuscripta Mathematica 100(4) (1999),
455-468.
DOI: https://doi.org/10.1007/s002290050212
[11] P. Deligne, La conjecture de Weil: II, Publications
Mathématiques de l’Institut des Hautes Études
Scientifiques 52(1) (1980), 137-252.
DOI: https://doi.org/10.1007/BF02684780
[12] P. Deligne and J. S. Milne, Tannakian Categories, In: Hodge
Cycles, Motives, and Shimura Varieties, Lecture Notes in Mathematics,
900, Springer-Verlag, 2nd Corrected Printing (1989), 101-228.
[13] N. D. Elkies, The existence of infinitely many supersingular
primes for every elliptic curve over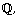 
Inventiones Mathematicae 89(3) (1987),
561-567.
DOI: https://doi.org/10.1007/BF01388985
[14] N. D. Elkies, Supersingular primes for elliptic curves over real
number fields, Compositio Mathematica 72(2) (1989), 165-172.
[15] V. Ertl, A new proof of a vanishing result due to Berthelot,
Esnault, and Rülling, Appear in Journal of Number Theory (2019).
DOI: https://doi.org/10.1016/j.jnt.2019.03.022
[16] H. Esnault, Varieties over a finite field with trivial Chow group
of o-cycles have a rational point, Inventiones Mathematicae 151(1)
(2003), 187-191.
DOI: https://doi.org/10.1007/s00222-002-0261-8
[17] J.-Y. Étesse and B. Le Stum, Fonctions L associées
aux F-isocristaux surconvergents: I, Interprétation
cohomologique, Mathematische Annalen 296(1) (1993), 557-576.
DOI: https://doi.org/10.1007/BF01445120
[18] R. Friedman, Global smoothings of varieties with normal
crossings, Annals of Mathematics 118(1) (1983), 75-114.
DOI: https://doi.org/10.2307/2006955
[19] W. Fulton, A fixed point formula for varieties over finite
fields, Mathematica Scandinavica 42 (1978), 189-196.
DOI: https://doi.org/10.7146/math.scand.a-11747
[20] E. Freitag and R. Kiehl, Etale Cohomology and the Weil
Conjecture, Ergebnisse der Mathematik und Ihrer Grenzgebiete, 3,
Springer-Verlag, 1988.
DOI: https://doi.org/10.1007/978-3-662-02541-3
[21] T. Fujisawa and C. Nakayama, Mixed Hodge structures on log
deformations, Rendiconti del Seminario Matematico della UniversitÃ
di Padova 110 (2003), 221-268.
[22] R. Friedman and F. Scattone, Type III degenerations of K3
surfaces, Inventiones Mathematicae 83(1) (1986), 1-39.
DOI: https://doi.org/10.1007/BF01388751
[23] K. Fujiwara and K. Kato, Logarithmic etale topology theory,
Preprint (1995).
[24] Y. Gongyo, Y. Nakamura and H. Tanaka, Rational points on log Fano
threefolds over a finite field, Preprint, Available from
arXiv:1512.05003v3.
[25] M. Hazewinkel, Formal Groups and Applications, Pure and Applied
Mathematics Series, Academic Press, New York, 1978.
[26] O. Hyodo and K. Kato, Semi-stable reduction and crystalline
cohomology with logarithmic poles, In: Périodes p-Adiques,
Seminaire de Bures, 1988, Astérisque 223, Soc. Math. de France
(1994), 221-268.
[27] W. Haboush and N. Lauritzen, Varieties of unseparated flags,
linear algebraic groups and their representations (Los Angeles, 1992),
Amer. Math. Soc. (1993), 35-57.
[28] L. Illusie, Complexe de de Rham-Witt et cohomologie cristalline,
Annales scientifiques de l’École Normale Supérieure, 4e
Série 12(4) (1979), 501-661.
DOI: https://doi.org/10.24033/asens.1374
[29] L. Illusie, An overview of the work of K. Fujiwara, K. Kato and
C. Nakayama on logarithmic étale cohomology, Societe Mathematique
de France, Asterisque 279 (2002), 271-322.
[30] K. Joshi, Exotic torsion, Frobenius splitting and the slope
spectral sequence, Canadian Mathematical Bulletin 50(4) (2007),
567-578.
DOI: https://doi.org/10.4153/CMB-2007-054-9
[31] K. Kato, Logarithmic structures of Fontaine-Illusie, In:
Algebraic Analysis, Geometry, and Number Theory, Johns Hopkins
University Press (1989), 191-224.
[32] K. Kato, Toric singularities, American Journal of Mathematics
116(5) (1994), 1073-1099.
DOI: https://doi.org/10.2307/2374941
[33] N. M. Katz, On a theorem of Ax, American Journal of Mathematics
93(2) (1971), 485-499.
DOI: https://doi.org/10.2307/2373389
[34] M. Kim, A vanishing theorem for Fano varieties in positive
characteristic, Preprint, Available from arXiv:math/0201183v3.
[35] K. Kodaira, On a differential-geometric method in the theory of
analytic stacks, Proceedings of the National Academy of Sciences of
the United States of America 39(12) (1953), 1268-1273.
DOI: https://doi.org/10.1073/pnas.39.12.1268
[36] V. S. Kulikov, Degenerations of K3 surfaces and Enriques’
surfaces, Mathematics of the USSR-Izvestiya 11(5) (1977), 957-989.
DOI: https://doi.org/10.1070/IM1977v011n05ABEH001753
[37] K. Kato and C. Nakayama, Log Betti cohomology, log étale
cohomology, and log de Rham cohomology of log schemes over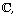 
Kodai Mathematical Journal 22(2) (1999),
161-186.
DOI: https://doi.org/10.2996/kmj/1138044041
[38] C. Liedtke, Lectures on supersingular K3 surfaces and the
crystalline Torelli theorem, In K3 Surfaces and their Moduli, Progress
in Mathematics 315 (2016), 171-235.
DOI: https://doi.org/10.1007/978-3-319-29959-4_8
[39] N. Lauritzen and A. P. Rao, Elementary counterexamples to Kodaira
vanishing in prime characteristic, Proceedings of the Indian Academy
of Sciences - Mathematical Sciences 107(1) (1997), 21-25.
DOI: https://doi.org/10.1007/BF02840470
[40] Y. Matsumoto, Good reduction criterion for K3 surfaces,
Mathematische Zeitschrift 279(1-2) (2015), 241-266.
DOI: https://doi.org/10.1007/s00209-014-1365-8
[41] A. Mokrane, La suite spectrale des poids en cohomologie de
Hyodo-Kato, Duke Mathematical Journal 72(2) (1993), 301-337.
DOI: https://doi.org/10.1215/S0012-7094-93-07211-0
[42] D. Mumford, Pathologies of modular algebraic surfaces, American
Journal of Mathematics 83(2) (1961), 339-342.
DOI: https://doi.org/10.2307/2372959
[43] D. Mumford, Bi-extensions of formal groups, In: Bombay Colloquium
on Algebraic Geometry, Oxford University Press (1969), 307-322.
[44] V. B. Mehta and A. Ramanathan, Frobenius splitting and cohomology
vanishing for Schubert varieties, Annals of Mathematics 122(1) (1985),
27-40.
DOI: https://doi.org/10.2307/1971368
[45] C. Nakayama, Degeneration of l-adic weight spectral
sequences, American Journal of Mathematics 122(4) (2000), 721-733.
DOI: https://doi.org/10.1353/ajm.2000.0030
[46] Y. Nakkajima, Liftings of log K3 surfaces and classical log
Enriques surfaces in mixed characteristics, Journal of Algebraic
Geometry 9 (2000), 355-393.
[47] Y. Nakkajima, p-adic weight spectral sequences of log
varieties, Journal of Mathematical Sciences, The University of Tokyo
12(4) (2005), 513-661.
[48] Y. Nakkajima, Signs in weight spectral sequences,
monodromy-weight conjectures, log Hodge symmetry and degenerations of
surfaces, Rendiconti del Seminario Matematico della Università di
Padova 116 (2006), 71-185.
[49] Y. Nakkajima, Weight filtration and slope filtration on the rigid
cohomology of a variety in characteristic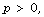 
Mémoires de la Société Mathématique
de France 130-131 (2012), pp 256.
DOI: https://doi.org/10.24033/msmf.441
[50] Y. Nakkajima, Artin-Mazur heights and Yobuko heights of proper
log smooth schemes of Cartier type, and Hodge-Witt decompositions and
Chow groups of quasi-F-split threefolds, Preprint, Available
from arXiv:1902.00185.
[51] Y. Nakkajima, Limits of weight filtrations and limits of slope
filtrations on infinitesimal cohomologies in mixed characteristics I,
Preprint, Available from arXiv:1902.00182.
[52] Y. Nakkajima, Monodromies and weight filtrations, and simple
normal crossing log surfaces with torsion canonical sheaves,
Preprint.
[53] N. Nygaard, On the fundamental group of a unirational 3-fold,
Inventiones Mathematicae 44(1) (1978), 75-86.
DOI: https://doi.org/10.1007/BF01389903
[54] Y. Nakamura and H. Tanaka, A Witt Nadel vanishing theorem for
threefolds, Preprint, Available from arXiv:1712.07358v1.
[55] Y. Nakkajima and F. Yobuko, Degenerations of log Hodge de Rham
spectral sequences, log Kodaira vanishing theorem in characteristic
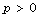and log weak Lefschetz conjecture for log
crystalline cohomologies, Preprint, Available from
arXiv:1902.09110v2.
[56] M. Papikian, Honda-Tate theorem for elliptic curves, Preprint,
Available from.
http://www.math.psu.edu/papikian/Research/HTS.pdf
[57] M. Raynaud, Contre-exemple au “vanishing theorem†en
caracteristique 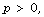C. P. Ramanujam– A Tribute, Tata
Institute of Fundamental Research Studies in Mathematics,
Springer-Verlag (1978), 273-278.
[58] M. Schlessinger, Functors of Artin rings, Transactions of the
American Mathematical Society 130(2) (1968), 208-222.
DOI: https://doi.org/10.1090/S0002-9947-1968-0217093-3
[59] N. I. Shepherd-Barron, Fano threefolds in positive
characteristic, Compositio Mathematica 105(3) (1997), 237-265.
DOI: https://doi.org/10.1023/A:1000158618674
[60] J. H. Silverman, The Arithmetic of Elliptic Curves (2nd Edition),
Graduate Texts in Mathematics 106, Springer-Verlag, 2009.
[61] J. H. Silverman, Advanced Topics in the Arithmetic of Elliptic
Curves, Graduate Texts in Mathematics 151, Springer-Verlag, 1994.
[62] J. Stienstra, Formal group laws arising from algebraic varieties,
American Journal of Mathematics 109(5) (1987), 907-925.
DOI: https://doi.org/10.2307/2374494
[63] J. Tate, Algebraic cycles and poles of zeta functions, In:
Arithmetic Algebraic Geometry, Harper and Row, New York (1965),
93-110.
[64] J. Tate, Endomorphisms of abelian varieties over finite fields,
Inventiones Mathematicae 2(2) (1966), 134-144.
DOI: https://doi.org/10.1007/BF01404549
[65] B. Totaro, The failure of Kodaira vanishing for Fano varieties,
and terminal singularities that are not Cohen-Macaulay, Preprint,
Available from arXiv:1710.04364v1.
[66] T. Tsuji, Poincaré duality for logarithmic crystalline
cohomology, Compositio Mathematica 118(1) (1999), 11-41.
DOI: https://doi.org/10.1023/A:1001020809306
[67] G. Van der Geer and T. Katsura, On a stratification of the moduli
of K3 surfaces, Journal of the European Mathematical Society 2(3)
(2000), 259-290.
DOI: https://doi.org/10.1007/s100970000021
[68] G. Van der Geer and T. Katsura, On the height of Calabi-Yau
varieties in positive characteristic, Documenta Mathematica 8 (2003),
97-113.
[69] F. Yobuko, Quasi-Frobenius splitting and lifting of Calabi-Yau
varieties in characteristic p, Mathematische Zeitschrift
292(1-2) (2019), 307-316.
DOI: https://doi.org/10.1007/s00209-018-2198-7
[70] J.-D. Yu and N. Yui, K3 surfaces of finite height over finite
fields, Journal of Mathematics of Kyoto University 48(3) (2008),
499-519.
DOI: https://doi.org/10.1215/kjm/1250271381
[71] D. Wan, Arithmetic mirror symmetry, Pure and Applied Mathematics
Quarterly, (Special Issue: In memory of Armand Borel, Part 1 of 3),
1(2) (2005), 369-378.
DOI: http://dx.doi.org/10.4310/PAMQ.2005.v1.n2.a7
[72] D. Wan, Mirror symmetry for zeta functions, Preprint, Available
from arXiv:math/0411464.
[73] W. C. Waterhouse, Abelian varieties over finite fields, Annales
Scientifiques de l’École Normale Supérieure, 4e Série
2(4) (1969), 521-560.
