Journal of Algebra, Number Theory: Advances and Applications[1] F. Chyzak, A. Quadrat and D. Robertz, Effective algorithms for
parametrizing linear control systems over ore algebras, Appl. Algebra
Engrg. Comm. Comput. 16(5) (2005), 319-376.
[2] T. Cluzeau and A. Quadrat, Factoring and decomposing a class of
linear functional systems, Lin. Alg. and its Appl. 428(1) (2008),
324-381.
[3] P. Cohn, Free Ideal Rings and Localizations in General Rings,
Cambridge University Press, 2006.
[4] H. Fujita, Global and Krull dimensions of quantum Weyl algebras,
Journal of Algebra 216(2) (1999), 405-416.
[5] C. Gallego, Matrix Methods for Projective Modules Over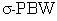 
Extensions, Ph.D. Thesis, Universidad
Nacional de Colombia, Bogotá, 2015.
[6] C. Gallego and O. Lezama, Gröbner bases for ideals of skew PBW
extensions, Comm. in Algebra 39(1) (2011), 50-75.
[7] C. Gallego and O. Lezama, Matrix approach to noncommutative stably
free modules and Hermite rings, Algebra and Discrete Mathematics 18(1)
(2014), 110-139.
[8] C. Gallego and O. Lezama, d-Hermite rings and skew PBW
extensions, São Paulo Journal of Mathematical Sciences (First
online: 25 August 2015), 1-13.
[9] C. Gallego and O. Lezama, Projective modules and Gröbner bases
for skew PBW extensions (to appear in Algebraic and Symbolic
Computation Methods in Dynamical Systems in the Springer series
Advances in Delays and Dynamics).
[10] J. Gago-Vargas, Bases for projective modules in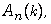 
J. Symb. Comp. 36 (2003), 845-853.
[11] T. Y. Lam, Serre’s Problem on Projective Modules, Springer
Monographs in Mathematics, Springer, 2006.
[12] T. Y. Lam, Lectures on Modules and Rings, Springer Graduate Text
in Mathematics 189, 1999.
[13] O. Lezama, Matrix and Gröbner Methods in Homological Algebra
over Commutative Polynomial Rings, Lambert Academic Publishing,
2011.
[14] O. Lezama and M. Reyes, Some homological properties of skew PBW
extensions, Comm. in Algebra 42 (2014), 1200-1230.
[15] A. Quadrat and D. Robertz, Computation of bases of free modules
over the Weyl algebras, J. Symb. Comp. 42 (2007), 1113-1141.
[16] J. T. Stafford, Module structure of Weyl algebras, J. London
Math. Soc. 18 (1978), 429-442.
