Journal of Algebra, Number Theory: Advances and Applications
OVER A FINITE FIELD[1] G. K. Bakshi and M. Raka, A class of constacyclic codes over a
finite field, Finite Fields Appl. 18(2) (2012), 362-377.
[2] T. Blackford, Negacyclic duadic codes, Finite Fields Appl. 14(4)
(2008), 930-943.
[3] T. Blackford, Isodual constacyclic codes, Finite Fields Appl. 24
(2013), 29-44.
[4] Bocong Chen, Yun Fan, Liren Lin and Hongwei Liu, Constacyclic
codes over finite fields, Finite Fields Appl. 18(6) (2012),
1217-1231.
[5] H. Q. Dinh, Repeated-root constacyclic codes of length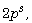 
Finite Fields Appl. 18(1) (2012),
133-143.
[6] H. Q. Dinh, Structure of repeated-root constacyclic codes of
length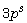 
and their duals, Discrete Mathematics 313
(2013), 983-991.
[7] H. Q. Dinh, On repeated-root constacyclic codes of length
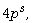Asian-European J. Math. 06, 1350020
(2013), [25 pages].
[8] A. Sahni and P. T. Sehgal, Minimal cyclic codes of length
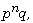Finite Fields Appl. 18 (2012),
1017-1036.
[9] A. Sahni and P. T. Sehgal, Enumeration of self dual and self
orthogonal negacyclic codes over finite fields, Advances in
Mathematics of Communications 9(4) (2015) 437-447.
[10] A. Sahni and P. T. Sehgal, Hermitian self-orthogonal constacyclic
codes over finite fields, Journal of Discrete Mathematics 985387
(2014), [7 pages].
