Journal of Algebra, Number Theory: Advances and Applications[1] C. W. Curtis and K. R. Reiner, Methods of Representation Theory
with Applications to Finite Groups and Orders, Vol. 1, John Wiley &
Sons, New York, 1981.
[2] P. J. Hilton and U. Stammbach, A Course in Homological Algebra,
Graduate Texts in Mathematics 4, Berlin-Heidelberg-New York, 1971.
[3] F. Jarquín-Zárate and G. Villa-Salvador, Cohomología y
Jacobianos, Aportaciones Matemáticas 37 (2007), 67-84.
[4] F. Jarquín-Zárate and G. Villa-Salvador, Integral representation
of generalized Jacobians, International Journal of Algebra 3(16)
(2009), 747-774.
[5] G. Karpilovsky, Group Representations, North-Holland Mathematics
Studies, 175 Vol. I, North-Holland, Amsterdam-London-New York-Tokyo,
1992.
[6] P. R. López-Bautista and G. D. Villa-Salvador, Integral
representation of p-class groups in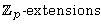 
and the Jacobian variety, Can. J. Math. 50
(1998), 1253-1272.
[7] V. J. Mejía-Huguet and M. Rzedowski-Calderón, Galois modular
representation of associated Jacobians in the Tamely ramified cyclic
case, Manuscripta Math. 126 (2008), 531-543.
[8] S. Morris, Pontryagin Duality and the Structure of Locally Compact
Abelian Groups, Cambridge University Press, Cambridge, 1977.
[9] M. Rzedowski-Calderón, G. D. Villa-Salvador and M. L. Madan,
Galois module structure of Tate modules, Math. Z. 224 (1997),
77-101.
[10] M. Rzedowski-Calderón and G. D. Villa-Salvador, Galois module
structure of Jacobians in unramified extensions, Journal of Algebra
242 (2001), 550-560.
[11] J. P. Serre, Local Fields, Graduate Texts in Mathematics 67,
Springer-Verlag, Berlin/Heidelberg/New York, 1979.
[12] J. P. Serre, Algebraic Groups and Class Fields, Graduate Texts in
Mathematics 117 Berlin/Heidelberg/New York, 1988.
[13] J. P. Serre, Galois Cohomology, Springer-Verlag,
Berlin-Heidelberg, 1997.
[14] R. Valentini, Representations of automorphisms on differentials
of function fields of characteristic p, J. Reine und Angew.
Math. 335 (1982), 164-179.
[15] R. Valentini, Some p-adic Galois representations for curves in
characteristic p, Math. Z. 192 (1986), 541-545.
[16] G. D. Villa-Salvador and M. L. Madan, Structure of semisimple
differentials and p-class groups in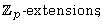 
Manuscripta Math. 57 (1987), 315-350.
[17] G. D. Villa-Salvador and M. L. Madan, Integral representations of
p-class groups in 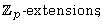semisimple differentials, and Jacobians,
Arch. Math. 56 (1991), 254-269.
[18] G. D. Villa-Salvador and M. Rzedowski-Calderón, Galois module
structure of generalized Jacobians, Revista Matemática de la
Universidad Complutense de Madrid 10 (1997), 39-51.
[19] G. D. Villa-Salvador, Introducción a la Teoría de las Funciones
Algebraicas, Fondo de Cultura Económica, México, 2003.
[20] G. D. Villa-Salvador, Topics in the Theory of Algebraic Function
Fields, Birkhäuser, Boston-Basel-Berlin, 2006.
[21] E. Weiss, Cohomology of Groups, Academic Press, New York/London,
1969.
