Journal of Algebra, Number Theory: Advances and Applications
ALGEBRA HOMOMORPHISMS[1] M. Amyari and M. S. Moslehian, Approximately ternary semigroup
homomorphisms, Lett. Math. Phys.77 (2006), 1-9.
[2] T. Aoki, On the stability of the linear transformation in Banach
spaces, J. Math. Soc. Japan 2 (1950), 64-66.
[3] C. Baak and M. S. Moslehian, Stability of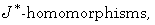 
Nonlinear Anal. TMA 63 (2005), 42-48.
[4] T. Bag and S. K. Samanta, Finite dimensional fuzzy normed linear
spaces, J. Fuzzy Math. 11(3) (2003), 687-705.
[5] N. Bazunova, A. Borowiec and R. Kerner, Universal differential
calculus on ternary algebras, Lett. Math. Phys. 67 (2004), 195-206.
[6] S. C. Cheng and J. N. Mordeson, Fuzzy linear operator and fuzzy
normed linear spaces, Bull. Calcutta Math. Soc. 86 (1994), 429-436.
[7] C. Felbin, Finite dimensional fuzzy normed linear space, Fuzzy
Sets and Systems 48 (1992), 239-248.
[8] P. Gavruta, A generalization of the Hyers-Ulam-Rassias stability
of approximately additive mappings, J. Math. Anal. Appl. 184 (1994),
431-436.
[9] D. H. Hyers, On the stability of the linear functional equation,
Proc. Nat. Acad. Sci. (USA) 27 (1941), 222-224.
[10] A. K. Katsaras, Fuzzy topological vector spaces II, Fuzzy Sets
and Systems 12 (1984), 143-154.
[11] S. V. Krishna and K. K. M. Sarma, Separation of fuzzy normed
linear spaces, Fuzzy Sets and Systems 63 (1994), 207-217.
[12] A. K. Mirmostafaee, M. Mirzavaziri and M. S. Moslehian, Fuzzy
stability of the Jensen functional equation, Fuzzy Sets and Systems
159 (2008), 730-738.
[13] M. S. Moslehian, Approximately vanishing of topological
cohomology groups, J. Math. Anal. Appl. 318(2) (2006), 758-771.
[14] A. Najati and A. Ranjbari, On homomorphisms between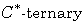 
algebra, J. Math. Ineq. 3 (2007),
387-407.
[15] Th. M. Rassias, On the stability of the linear mapping in Banach
spaces, Proc. Amer. Math. Soc. 72 (1978), 297-300.
[16] S. M. Ulam, Problems in Modern Mathematics, Science Editions,
Wiley, New York, 1964 (Chapter VI, Some Questions in Analysis: §1,
Stability).
[17] Congxin Wu and Jinxuan Fang, Fuzzy generalization of Klomogoroffs
theorem, J. Harbin Inst. Technol. 1 (1984), 1-7. (in Chinese, English
abstract)
[18] J.-Z. Xiao and X.-H. Zhu, Fuzzy normed spaces of operators and
its completeness, Fuzzy Sets and Systems 133 (2003), 389-399.
[19] H. Zettl, A characterization of ternary rings of operators, Adv.
Math. 48 (1983), 117-143.
