Author's: Nitis Mukhopadhyay and Bhargab Chattopadhyay
Pages: [93] - [130]
Received Date: April 20, 2011
Submitted by:
We consider unbiased estimation of 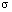 in a
in a 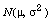 population. Traditional unbiased stimators
consist of appropriate multiples of both the sample standard deviation
S, that is,
population. Traditional unbiased stimators
consist of appropriate multiples of both the sample standard deviation
S, that is, 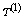 and Gini’s mean difference (GMD),
that is,
and Gini’s mean difference (GMD),
that is, 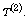 Both
Both 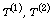 depend upon U-statistics associated
with symmetric kernels of degree two. In this paper, we develop a new
approach of constructing higher-order unbiased U-statistics
depend upon U-statistics associated
with symmetric kernels of degree two. In this paper, we develop a new
approach of constructing higher-order unbiased U-statistics
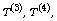 and
and 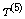 for
for 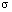 based upon symmetric kernels with degree
three, four, and four, respectively. From this investigation, we find
that the new unbiased estimators
based upon symmetric kernels with degree
three, four, and four, respectively. From this investigation, we find
that the new unbiased estimators 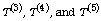 for
for 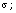 (i) go practically head-to-head with the
existing estimators
(i) go practically head-to-head with the
existing estimators 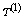 and
and 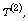 (ii)
(ii) 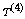 beats
beats 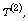 and (iii)
and (iii) 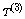 very nearly beats
very nearly beats 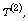 whether n is small or moderately
large. In other words, it is our belief that this new approach appears
very promising.
whether n is small or moderately
large. In other words, it is our belief that this new approach appears
very promising.
efficiency, exact variances, Gini’s mean difference, kernel’s degree higher than two, large-sample variances, population standard deviation, sample standard deviation, symmetric kernel, U-statistics, unbiased estimators.