Journal of Statistics: Advances in Theory and ApplicationsAuthor's: N. I. Badmus, Olanrewaju Faweya and K. A. Adeleke
Pages: [1] - [33]
Received Date: October 10, 2020; Revised November 11, 2020
Submitted by:
DOI: http://dx.doi.org/10.18642/jsata_7100122158
In this article, we investigate a distribution called the generalized
beta-exponential Weibull distribution. Beta exponential x
family of link function which is generated from family of generalized
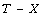distributions is used in generating the new
distribution. Its density and hazard functions have different shapes
and contains special case of distributions that have been proposed in
literature such as beta-Weibull, beta exponential,
exponentiated-Weibull and exponentiated-exponential distribution.
Various properties of the distribution were obtained namely; moments,
generating function, Renyi entropy and quantile function. Estimation
of model parameters through maximum likelihood estimation method and
observed information matrix are derived. Thereafter, the proposed
distribution is illustrated with applications to two different real
data sets. Lastly, the distribution clearly shown that is better
fitted to the two data sets than other distributions.
moments, information matrix, order statistics, quantile function,
Renyi entropy, distribution.
