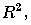Journal of Statistics: Advances in Theory and Applications
AND BIAS REDUCTION IN MATCHING
HIERARCHICAL DATA: A MONTE CARLO STUDYAuthor's: Qiu Wang, Kimberly S. Maier and Richard T. Houang
Pages: [43] - [81]
Received Date: March 9, 2017
Submitted by:
DOI: http://dx.doi.org/10.18642/jsata_7100121791
Based on a two-level structural equation model, this simulation study
examines how omitted variables affect estimation bias in matching
hierarchical data. Six simulated cases of omitted variables are
examined by manipulating level-1 and/or level-2 residual variances and
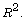Results show that (1) Mahalanobis
distance matching is less effective than propensity score matching;
(2) level-1 matching is less sensitive to omitted variables than
level-2 matching; (3) dual-matching (level-1 plus level-2 matching) is
robust to omitted variable problems; and (4) different sizes of
caliper should be used for level-1 and level-2 matching because
caliper matching depends on the data structure. To address the
challenges encountered when matching more complicated hierarchical
data with omitted variables, directions for future research are
suggested. This study can help researchers choose an appropriate
matching strategy to reduce selection bias for program evaluation when
hierarchically structured data are used.
propensity score matching, level-1 matching, level-2 matching, dual matching, omitted variables, structural equation modelling, multi-level, longitudinal data.
