Journal of Statistics: Advances in Theory and ApplicationsAuthor's: K. S. Madhava Rao and M Raghunath
Pages: [133] - [162]
Received Date: September 13, 2016
Submitted by:
DOI: http://dx.doi.org/10.18642/jsata_7100121717
In testing whether a treatment has an effect or not, the experimenter
is often obliged to use the same subjects for control and treated
groups. In such a case, it is generally unrealistic to assume
independence and one is led to tests of bivariate symmetry. In the
nonparametric setup, Hollander [3] proposed a conditionally
distribution-free test for bivariate symmetry based on the sample
distribution function. The hypothesis of interest considered by him
was that the bivariate random variables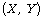 
are exchangeable or equivalently, the
hypothesis of treatment versus control. The equivalence between the
hypothesis of exchangeability and the hypothesis of conditional
symmetry about an axis is central to the motivation behind the
proposed test. The test is based on a measure of deviance between
observed counts of bivariate samples in suitably defined pairs of
sets. It is shown that the test is distribution-free and the exact
null distribution can be easily computed. For sample size from
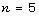up to 
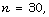the table of exact distribution is
provided. For sufficiently large n, a chi-square approximation
is provided. The empirical power of the proposed test is evaluated by
simulating samples from suitable classes of symmetric and asymmetric
bivariate distributions. It is shown that the test performs reasonably
well as compared to its parametric (Bell and Haller [1]) and
non-parametric competitors (Hollander [3] and Wilcoxon [8]).
bivariate symmetry, conditional symmetry, empirical power, non parametric test.
