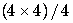Volume no :15, Issue no: 1, March (2016)

Journal of Statistics: Advances in Theory and Applications

APPLICATION OF ADJACENCY AND GENERALIZED INVERSE MATRICES TO ORDERING THE THREE OPTIMAL SEMI-LATIN SQUARES

Author's: N. P. Uto and P. E. Chigbu
Pages: [17] - [33]
Received Date: January 6, 2016
Submitted by:
DOI: http://dx.doi.org/10.18642/jsata_7100121618

Abstract

In this work, we present the adjacency and generalized inverse matrices of the three optimal 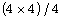semi-Latin squares. These matrices are then used in conjunction with each other to discriminate amongst the squares by computing and comparing the variance of adjacency induced by the treatments in each square with those of the other squares, with the aid of MATLAB. The square which minimizes both the maximum variance of adjacency and the number of distinct values of the variance of adjacency amongst the squares, and where tie occurs, also have a minimum value of this variance is considered most preferable, and so on. Results show that the square, 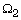is the most preferable for experimentation, while 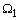is preferable to 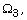which is consistent with earlier results by Uto and Chigbu [23].

Keywords

optimal design, optimality criteria, treatment contrasts, doubly-resolvable design, variety-concurrence graph, canonical efficiency factor, treatment concurrences.