Journal of Statistics: Advances in Theory and ApplicationsAuthor's: Murman Kintsurashvili, Tengiz Kiria and Gogi Pantsulaia
Pages: [179] - [233]
Received Date: March 19, 2015
Submitted by:
DOI: http://dx.doi.org/10.18642/jsata_7100121469
By using the notion of a Haar ambivalent set introduced by Balka et
al. [1], essentially new classes of statistical structures having
objective and strong objective estimates of unknown parameters are
introduced in a Polish non-locally-compact group admitting an
invariant metric and relations between them are studied in this paper.
An example of such a weakly separated statistical structure is
constructed for which a question asking “whether there exists a
consistent estimate of an unknown parameter” is not solvable within
the theory (ZF) & (DC). A question asking “whether
there exists an objective consistent estimate of an unknown parameter
for any statistical structure in a non-locally compact Polish group
with an invariant metric when subjective one exists” is answered
positively when there exists at least one such a parameter the
pre-image of which under this subjective estimate is a prevalent.
These results extend recent results of authors. Some examples of
objective and strong objective consistent estimates in a compact
Polish group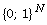 
are considered in this paper.
an objective infinite-sample consistent estimate, shy set, Haar ambivalent set, Polish group.
