Volume no :13, Issue no: 1, March (2015)

Journal of Statistics: Advances in Theory and Applications

A GEOMETRIC APPROACH TO CANCER GROWTH PREDICTION BASED ON COX PROCESSES

Author's: Iulian T. Vlad and Jorge Mateu
Pages: [1] - [32]
Received Date: December 11, 2014
Submitted by:
DOI: http://dx.doi.org/10.18642/jsata_7100121428

Abstract

Lévy theory provides a potential mathematical framework to model space and space-time stochastic processes. In addition, spatial point processes define stochastic models for random patterns of points in 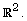These processes play a special role in stochastic geometry as the building blocks of more complicated random set models. In this paper, we focus on a family of Lévy-based spatial Cox processes to model and predict tumor growth. We develop a procedure to simulate the growing of tumors. This algorithm can be used to study the evolution in time of any 2- and 3-dimensional geometrical forms such as cancer skin and all type of boundary evolution. We analyze real data and show that the procedure developed works fine and is useful for prediction purposes.

Keywords

cobweb algorithm, Cox processes, space-time modelling, tumor growth.