Journal of Algebra, Number Theory: Advances and Applications
Author's: GEORGES GRAS
Pages: [57] - [94]
Received Date: March 13, 2012
Submitted by:
Let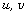 
be coprime integers such that 
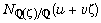is the p-th power of an integer,
where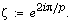 
Using the Brückner-Vostokov explicit
formula, we establish a product formula for the p-th power
residue symbols computed in our article in common with Quême [7].
This product formula is equivalent to the relations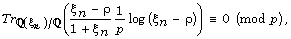 
for all 
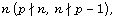where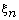 
is a primitive n-th root of unity,
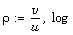is the p-adic logarithm. This
allows us to verify, for given values of p, the insolubility of
the above equation under the assumption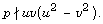 
This insolubility is then equivalent to the
existence of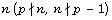 
such that 
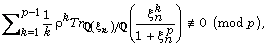constituting an alternative to
Kummer-Mirimanoff congruences without any reference to Bernoulli
numbers (see Sections 5, 6, 7). For instance, for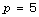 
and the only possible classes 
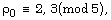the above condition is fulfilled for
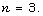For 
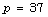and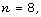 
the condition is fulfilled for all
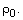
Diophantine equations, cyclotomic fields, cyclotomic units, class field theory, reciprocity laws, Fermat’s last theorem, Mirimanoff congruences.
