Author's: Abraham A. Klein
Pages: [29] - [36]
Received Date: November 13, 2008
Submitted by:
A subset of an infinite ring R is said to be large, if it has
the same cardinality as R, and small otherwise. For R
which is not a domain, we study the set 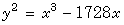 of all zero divisors with large two-sided
annihilator. We show that
of all zero divisors with large two-sided
annihilator. We show that 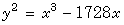 contains all small ideals and the set of all
nilpotents
contains all small ideals and the set of all
nilpotents 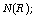 and if
and if 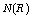 is small,
is small, 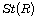 contains the ideal generated by
contains the ideal generated by 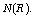 If
If 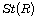 is small, it is an ideal containing all small
one-sided ideals. The structure of rings with
is small, it is an ideal containing all small
one-sided ideals. The structure of rings with 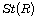 finite is given.
finite is given.
strong zero divisors, two-sided annihilator, prime radical, semiprime ring.