Journal of Algebra, Number Theory: Advances and Applications
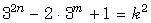
Author's: Gervasio G. Bastos and Diego Marques
Pages: [91] - [103]
Received Date: November 27, 2010
Submitted by:
In 1981, Beukers used a hypergeometric method for proving that the
well-known generalized Ramanujan-Nagell equation
has at most one solution in positive integers x and n,
where C and p are previously fixed, with a few
exceptions.
In this note, we give an elementary proof of this result when n is
even as well as the complete solution of a such equation when C
is a power of 2009. Moreover, we prove that the previous result is
surprisingly connected with the title equation, which allow us to find
all solutions for that equation.
Diophantine equation, linear forms in logarithms, Baker-Davenport, Ramanujan-Nagell.
