Author's: Tarek Sayed Ahmed
Pages: [19] - [40]
Received Date: June 14, 2009
Submitted by:
We study expansions of (representable) cylindric algebras 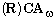 that are reducts of polyadic equality
algebras. The question we adress is: Can we add finitely many
substitutions, so that in the expanded language of
that are reducts of polyadic equality
algebras. The question we adress is: Can we add finitely many
substitutions, so that in the expanded language of 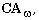 there is a finite set of quantifier free
formulas that force representability of the cylindric reduct of
algebras satisfying them. A refinement of a known positive solution
(with a new proof) is presented. On the other hand, we show that if we
expand the language of
there is a finite set of quantifier free
formulas that force representability of the cylindric reduct of
algebras satisfying them. A refinement of a known positive solution
(with a new proof) is presented. On the other hand, we show that if we
expand the language of 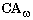 by finitely many substitutions
corresponding to bijections then, in the expanded language, no
quantifier free set of formulas containing only finitely many
variables axiomatize
by finitely many substitutions
corresponding to bijections then, in the expanded language, no
quantifier free set of formulas containing only finitely many
variables axiomatize 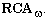
cylindric algebras.