Author's: Yongsheng Tang and Heqian Xu
Pages: [1] - [16]
Received Date: November 15, 2018
Submitted by:
DOI: http://dx.doi.org/10.18642/jantaa_7100122020
Let 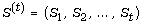 be a linear recurring sequence over
be a linear recurring sequence over 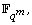 where each
where each 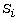 is a linear recurring sequence over
is a linear recurring sequence over 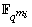 with minimal polynomial
with minimal polynomial 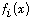 over
over 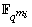 and the finite field
and the finite field 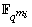 is a subfield of finite field
is a subfield of finite field 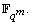 Let T be a linear transformation of
Let T be a linear transformation of
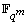 over
over 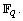 Denote
Denote 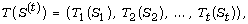 where
where 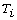 is a linear transformation of
is a linear transformation of 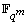 over
over 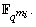 In this paper, we study the minimal polynomial
and linear complexity of linear recurring sequence
In this paper, we study the minimal polynomial
and linear complexity of linear recurring sequence 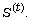 If the canonical factorization of each
If the canonical factorization of each
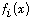 in
in 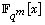 is known, we determine the minimal polynomial
and linear complexity of linear recurring sequence
is known, we determine the minimal polynomial
and linear complexity of linear recurring sequence 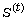 over
over 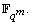 Furthermore, we determine the minimal
polynomial of
Furthermore, we determine the minimal
polynomial of 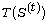 if the minimal polynomial of each
if the minimal polynomial of each 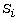 without multiple roots is known.
without multiple roots is known.
linear recurring sequences, linear complexity, minimal polynomial.