Journal of Algebra, Number Theory: Advances and ApplicationsAuthor's: Elliot Benjamin
Pages: [79] - [91]
Received Date: March 31, 2018; Revised April 28, 2018
Submitted by:
DOI: http://dx.doi.org/10.18642/jantaa_7100121949
Let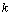 
be a real quadratic number field with 2-class
group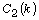 
isomorphic to 
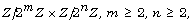such that the discriminant of 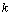is divisible by only positive prime
discriminants. Let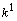 
be the Hilbert 2-class field of 
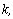and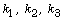 
be the three unramified quadratic extensions of
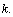We prove that if the 2-class number of
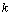is equal to the 2-class number of 
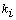for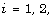 
and 3, then either 
or rank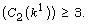 
real quadratic number field, Hilbert 2-class field, discriminant, 2-rank, unramified quadratic extension, commutator subgroup, noncyclic class group.
