Journal of Algebra, Number Theory: Advances and ApplicationsAuthor's: Luc E. F. Diékouam, Yannick L. T. Jeufack, Étienne R. A. Temgoua and Marcel Tonga
Pages: [29] - [83]
Received Date: March 20, 2017
Submitted by:
DOI: http://dx.doi.org/10.18642/jantaa_7100121803
The structure of the lattice of clones on a finite set has been proven
to be very complex. To better understand the top of this lattice, it
is important to provide a characterization of submaximal clones in the
lattice of clones. It is known that the clones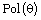 
and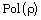 
(where 
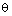is a nontrivial equivalence relation on
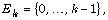and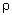 
belongs to one of the six types of
relations which characterize maximal clones) are maximal clones. In
this paper, we provide a classification of relations (of
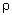Rosenberg’s list) on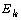 
for which the clone 
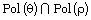is maximal in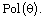 
clones, submaximal, equivalence relations, maximal.
