Volume no :15, Issue no: 2, June (2016)

Journal of Algebra, Number Theory: Advances and Applications

MATRIX COMPUTATIONS ON PROJECTIVE MODULES USING NONCOMMUTATIVE GRÖBNER BASES

Author's: Claudia Gallego
Pages: [101] - [139]
Received Date: July 11, 2016
Submitted by:
DOI: http://dx.doi.org/10.18642/jantaa_7100121686

Abstract

Constructive proofs of fact that a stably free left S-module M with 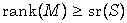is free, where sr(S) denotes the stable rank of an arbitrary ring S, were developed in [7] (see also [5] and [15]). Additionally, in such papers, are presented algorithmic proofs for calculating projective dimension, and to check whether a left S-module M is stably free. Given a left A-module M, with A a bijective skew PBW extension, we will use these results and Gröbner bases theory, to establish algorithms that allow us to calculate effectively the projective dimension for this module, to check whether is stably free, to construct minimal presentations, and to obtain bases for free modules.

Keywords

noncommutative Gröbner bases, skew PBW extensions, stably free modules, free modules, computation of bases, constructive algorithms.