Journal of Algebra, Number Theory: Advances and ApplicationsAuthor's: Werner Hürlimann
Pages: [77] - [100]
Received Date: March 22, 2016
Submitted by:
DOI: http://dx.doi.org/10.18642/jantaa_7100121649
The number of distinct zero-free primitive square representations by
the ternary quadratic form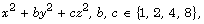s 
is expressed in terms of the number of
primitive square representations by this form taking into account
zeros, permutations and sign changes, and the number of distinct
primitive square representations by certain binary quadratic forms.
Asymptotic expressions for the cumulative numbers are also derived and
the obtained formulas are illustrated at two typical cases.
sum of squares primitive representation, ternary quadratic form, twisted Euler function, Bell ternary quadratic form, Cooper and Lam’s conjecture.
