Journal of Algebra, Number Theory: Advances and ApplicationsAuthor's: V. I. Danilov, A. V. Karzanov and G. A. Koshevoy
Pages: [89] - [106]
Received Date: December 28, 2015
Submitted by:
DOI: http://dx.doi.org/10.18642/jantaa_7100121613
Studying quasicommuting flag minors of a quantum matrix, Leclerc and
Zelevinsky introduced the notion of weakly separated collections of
subsets of the set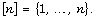 
Answering their conjectures on such
collections, there have been proved that some natural domains
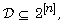in particular, the Boolean cube
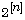and the discrete Grassmannian 
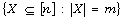for 
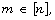possess the property of purity, which
means that all inclusion-wise maximal weakly separated collections in
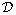have the same size.
In this note, we prove the purity for a class of domains generalizing
Boolean cubes and discrete Grassmannians. It is generated by so-called
steep ladder diagrams.
quasicommuting quantum minors, weakly separated sets, strongly separated sets, lattice paths.
