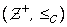Journal of Algebra, Number Theory: Advances and Applications
AND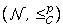 
Author's: Sankar Sagi
Pages: [93] - [102]
Received Date: January 31, 2014
Submitted by:
A convolution is a mapping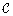 
of the set 
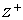of positive integers into the set
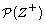of all subsets of 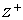such that, for any 
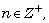each member of 
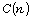is a divisor of n. If 
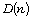is the set of all divisors of n,
for any n, then D is called the Dirichlet’s
convolution. If 
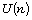is the set of all unitary (square free)
divisors of n, for any n, then U is called
unitary (square free) convolution. Corresponding to any general
convolution C, we can define a binary relation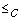 
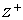on by ‘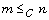
if and only if 
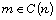’. In this paper, we present a
correspondence between the filters in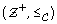 
and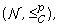 
where 
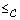is the binary relation induced by the
convolution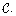 
partial order, lattice, filter, convolution, multiplicative.
