Journal of Algebra, Number Theory: Advances and ApplicationsAuthor's: Fausto JarquÃn Zárate and Gabriel Villa Salvador
Pages: [99] - [128]
Received Date: December 2, 2009
Submitted by:
Let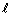 
be a prime number and let 
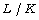be a finite Galois 
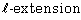of function fields of one variable with
field of constants k, an algebraically closed field of
characteristic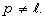 
In this paper, we obtain two explicit
characterizations of the non-injective component of the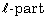 
of the generalized Jacobian 
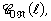where the modulus 
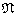in L is induced by a modulus
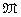in K, which contains in its support
all the prime divisors of K ramified in L. We find
explicitly the decomposition of the dual of the 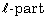of the generalized Jacobian 
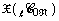as direct sum of indecomposable 
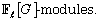We determine an exact sequence of 
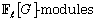that characterizes implicitly the 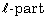of the usual Jacobian 
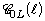in the general case.
Tate cohomology group, Galois modules, Jacobian, class groups, injective modules, integral representation, modular representation.
