Journal of Algebra, Number Theory: Advances and ApplicationsAuthor's: George Szeto and Lianyong Xue
Pages: [21] - [26]
Received Date: September 25, 2009
Submitted by:
Let R be a ring with 1,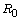 
the center of R, G a group,
RG a group ring of G over R, and C the
center of RG. If RG is Azumaya, then so is RK for
every subgroup K of G. For a subgroup K of finite
order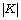 
invertible in R, if RG is
Azumaya, then RG is a Hirata separable extension of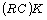 
and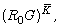 
respectively, which are direct summands of
RG as bimodules over themselves, where 
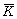is the inner automorphism group of the group
ring RG induced by the elements of K. Also, for any
subgroup K of G, the converse holds.
group rings, separable extensions, Azumaya algebras, Hirata separable extensions.
