Journal of Algebra, Number Theory: Advances and ApplicationsAuthor's: ADEL ALAHMADI, MICHEL PLANAT and PATRICK SOLÉ
Pages: [41] - [55]
Received Date: August 14, 2012
Submitted by:
The oscillations of the prime counting function 
around the logarithmic integral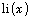 
are known to be controlled by the zeros of
Riemann’s zeta function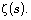 
Similarly, the discrepancy 
between the number of primes modulo
q in a quadratic residue class R and in a quadratic
nonresidue class N-the so-called Chebyshev’s bias- is
controlled by the zeros of a Dirichlet L-function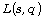 
with the modulus q. In this work,
we introduce a new bias, called the regularized Chebyshev’s
bias, whose non-negativity is expected to be equivalent to a Riemann
hypothesis for 
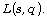In particular, under the generalized
Riemann hypothesis, this new bias should be positive for all integers
q. The results are motivated and illustrated by extensive
numerical calculations.
prime counting, Chebyshev functions, generalized Riemann hypothesis.
