Journal of Algebra, Number Theory: Advances and ApplicationsAuthor's: Tarek Sayed Ahmed
Pages: [113] - [125]
Received Date: June 13, 2009
Submitted by:
Let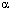 
be an infinite ordinal. There are
non-isomorphic representable algebras of dimension 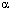each of which is a generating subreduct of
the same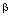 
dimensional algebra. Dually there exists a
representable algebra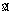 
of dimension 
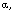such that 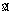is a generating subreduct of 
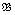and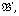 
however, 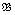and 
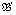are not isomorphic. The above was proven to
hold for infinite dimensional cylindric algebras
(CA’s) in [3] answering questions raised by
Henkin et al. In this paper, we investigate the analogous statements
for algebraisations other than cylindric algebras. We show that
Pinter\'s substitution algebras and Halmos’ quasi-polyadic
algebras behave like CA’s, however, Halmos
polyadic algebras do not.
algebraic logic, neat reducts, super amalgamation.
